삼각함수를 쉽게 배워봅시다. #6 - 나도 삼각함수 그래프를 유도 할 수 있다!
Posted on 2009. 7. 3. 11:41
Filed Under Programming/설계+분석+이론
<출차: http://blog.naver.com/azu016/110045274891 >
1. 일단 삼각함수의 sin, cos, tan 에 대해 생각해 봅시다.
길고 어렵게 설명하지 않겠습니다. 그런만큼 수학적으로 설명이 애매하거나 오류가 있을 수도 있겠지요.
가볍게 설명한다는 취지이고, 또 제 전공이 수학관련이 아닌만큼 애매한 설명이 있더라도 이해 부탁드립니다.
여기 단위원(반지름이 1인 원)이 있습니다.
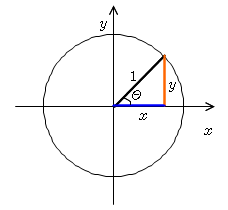
이 단위원의 반지름을 기준으로 삼각형을 그렸을때
![]()
라는 것은 다들 알고 계시죠?
아마 이 내용을 읽고 계시는 분들이라면 이것쯤은 다 알고 계실것으로 판단됩니다.
그럼 지금부터 이 내용을 알고 계신다는 전제 하에 설명을 시작하도록 하겠습니다.
지금부터 우리 할 일은 바로 이 박스안에 그림을 채워 넣는 일 입니다.
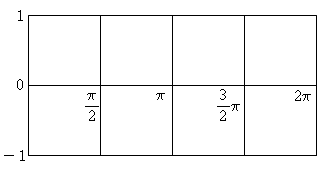
2. sin 그래프를 생각해보자.
앞서 보셨겠지만, sin은 어떻습니까? 분모는 1로 고정이 되어있고 분자는 y값이었죠? y값인 주황색 선에 주목하세요!
일단 1사분면인 0 ~ π/2 사이를 생각해 봅시다. 맨 처음에 세타(Θ)값은 0˚에서 출발하겠지요.
0˚ 일때는 y값이 존재하나요? 존재하지 않죠? 왜 존재하지 않냐구요?
각도가 없을테니 검은색 반지름선과 파란색 x축과 겹쳐 질 것 아니겠습니까? 그러면 주황색의 y값은 존재할까요? x축과 겹쳐있는데??
그림을 그리며 상상해보세요 ^^; 일단 y값이 0이라는 것을 알 수 있습니다. 그러면 sin 0˚는 0/1 = 0 이라는 것을 알게 되겠지요.
맨 처음에 시작하는 값은 0˚의 0이라는 값으로 시작합니다. 이제 점점 세타값인 각도에 변화를 줍시다.
각도를 크게 만들수록... 즉 세타값이 올라가면 올라 갈 수록 y값이 어떻게 되나요?
일단 y값이 x축보다 위에 있는 것을 보니 +값 인 것을 알 수 있네요. 그리고 막대기가 점점 길어진다는것. 값이 증가한다는것을 의미하죠?
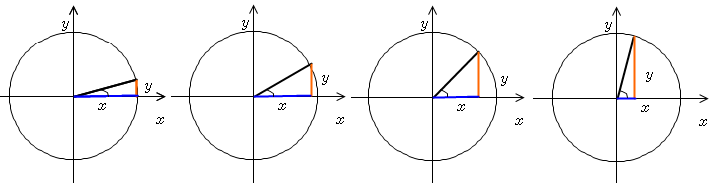
자 그러면 생각해 봅시다. 0˚ ~ 90˚ 구간. 분모는 1로 고정이 되어있는데.. 세타값을 늘리면 늘릴수록 y값(주황색선)이 어떻게 됩니까?
+값인데 그 값이 점점 커짐을 알 수 있습니다. 그리고 그렇게 증가해서 90˚가 되었을때 y값이 얼마가 되나요?
바로 반지름과 똑같은 1이 된다는 것을 알 수 있습니다. 그러면 우리가 아까 채워야 하는 박스안을 이렇게 채울 수 있겠지요?
0 → π/2까지 증가 할 수록 값은 0 → 1로 점점 커지고 있으니까 아래와 같이 박스를 채울 수 있겠지요? ㅋ
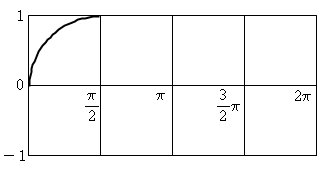
자. 0도와 π/2사이인 1사분면에 대해서는 분석이 끝났습니다. 그렴 2사분면인 π/2부터 π까지를 또 분석해 볼까요?
역시 sin값의 정의는 분모는 1. 분자는 y. 그러면 2사분면에서도 아까와 마찬가지로 y값이 어떻게 변화하는지만 찾아내면 두번째 칸도
자연스럽게 그림을 그려 나갈 수가 있겠지요? 자 그럼 다시 생각해 봅시다. 맨처음에 0이었던 y값이 점점 오르고 올라서 1이 되었습니다.
그럼 2사분면에서의 시작값은 1이 되겠지요. 각도가 증가 할 수록 어떻게 될까요? 직접 선을 따라 그려보시면 아시겠지요?
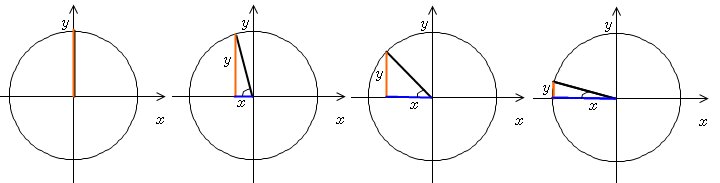
y값인 주황색선은 x축 위에 있으니까 +값이긴 한데.. 그 절대값이라 할 수 있는 길이가 점점 짧아지고 있습니다.
그 길이가 짧아져서 결국 각도가180˚ 파이(π)값이 되면 다시 0으로 돌아옴을 알 수 있습니다.. 그럼 상자에도 그림을 채울 수가 있겠지요.
π/2도 → π까지 증가 할 수록 값은 1 → 0로 점점 작아지고 있으니까..
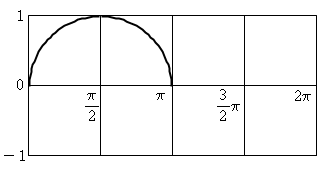
여기까지 이해가 되신거면 이제 다 따라오신겁니다. ㅎㅎ;; 3사분면 4사분면도 그대로 따라하시면 되겠습니다.
스스로 한 번 삼각형을 그려보세요. 3사분면은 어떻게 되나요? y값의 주황색선 그래프의 막대기가 길어지나요? 짧아지나요?
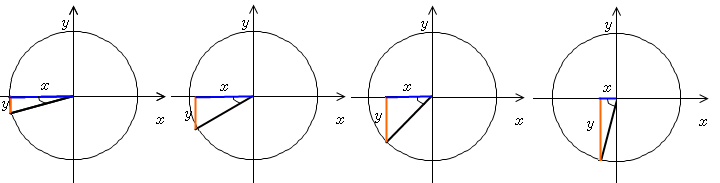
길어지고 있지요? 길어지긴 하는데.. 그 방향이 어디인가요? 바로 x축보다 아래로 증가하고 있다는 것 알 수 있나요?
그렇다면 x축 아래에 있으니까 -값이면서 막대기가 길어진다.. 즉 '마이너스값'이 '증가' 한다는 것을 알 수 있습니다.
π/2도 → 3π/2까지 증가 할 수록 막대기가 길어집니다. 막대기가 길어진다는건 값이 커진다는 의미!!
근데 그 방향이 어디다? 마이너스다! 즉 마이너스값이 점점 커지고 있으니까..
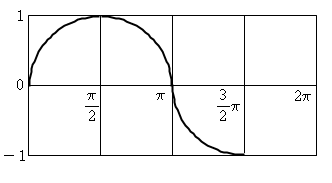
자 이제 다 채웠습니다!! 여기까지 이해 하셨다면 이제 4사분면 그리기도 쉽게 하실 수 있으실 겁니다. 자 4사분면 그리기는 숙제~
해설만 해드릴께요. y값(주황색선)이 점점 작아지고 있지요? 결국 어디로 돌아옵니까? 다시 0으로 돌아오는 것을 알 수 있지요?
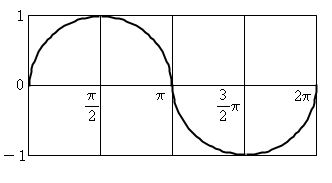

이렇게 sin곡선을 그려보았습니다. 어때요? 어려운 부분이 있었나요?
cos곡선 tan곡선도 위와 같은 방식으로 유도를 해 나가시면 되겠습니다.
cos곡선 같은경우에도 똑같습니다. 분모는 1로 고정이 되어있는데 아까와는 다르게 분자값만 x값으로 바뀐거 뿐이지요.
그럼 아까와 같이 똑같이 그릴 수 있겠지요? sin 에서는 y였던것이 cos에서는 x로 바뀐것 과 다름 없으니까요.

맨처음 x값은 1로 시작해서 세타값이 점점 커지면 커질수록 x값이 점점 어떻게 되나요? 점점 작아지고 있다는 것을 알 수 있지요?
1사분면의 경우 cos값의 경우 1로 시작해서 0으로 끝난다는 것을 알 수 있습니다.
2사분면의 경우 각도가 커지면 커질수록 파란색 x값의 길이가 길어지는게 보이시나요? 안보이신다구요?
아까 sin 그래프를 설명했을때 쓰던 그림을 보세요 ㅎㅎ; 이제 2사분면에서 각도가 커지면 커질수록 파란색선이 길어지는게 보이시죠?
근데 그 길어지는 값이 어떤가요? 점점 왼쪽으로 커진다는것은.. 무엇을 의미할까요? 바로 마이너스. 음수값이 커진다는 것이죠.
그러면 2사분면의 첫번째 값은 0으로 시작해서 -1로 끝난다는거 알 수 있나요?
3사분면은 각도가 커질수록 x값이 작아지고 있지요. -1에서 0으로 이동.
4사분면은 각도가 커질수록 x값이 커지는데.. 그 커지는 방향이 오른쪽이죠. +방향입니다.
이를 종합하면..
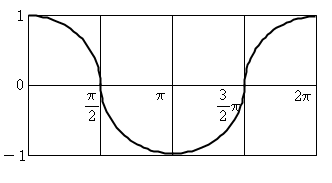
와 같은 그림을 그리실 수 있으실 겁니다. ^^;
tan 그리기가 어렵다고 느끼시는 분들이 많으실거 같은데요..
역시 같은 방법입니다.. 각 사분면에서 x값과 y값이 어떻게 변화하는지는 잘 캐치해 보세요 ^^;
중요한 것은 이것 입니다. 이 두가지만 생각하세요.
1. x값 또는 y값의 막대기가 길어지고 있느냐 짧아지고 있느냐. (절대값)
2. x값, y값이 어디에 몇 사분면에 위치하느냐. (부호) -> ex) 2사분면 x값은 -, y값은 + 3사분면 x값은 -, y값은 -
이 두가지를 생각하며 아래에 있는 탄젠트 그래프에 그려진 실선을 따라 그림을 잘 생각해 보세요.
그러면 그림이 이렇게 나오실 겁니다.^^;
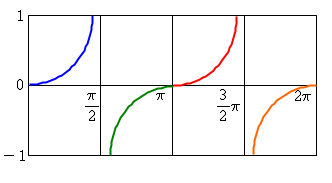
사실은 박스 위로도 선이 계속 증가해야 하지만 이해를 돕기위해 구간을 1 ~ -1만 잡았습니다.
이해를 돕기 위해 각 사분면 별로 색깔을 구별했습니다. 1사분면은 파란색, 2사분면은 녹색, 3사분면은 빨간색, 4사분면은 주황색입니다.
각 사분면 별로 그림이 저렇게 나올겁니다. 이렇게 보니까 그림이 뭔가 아니다 싶다구요?
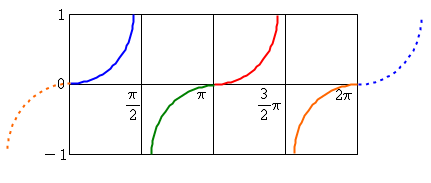
이렇게 보니까 이해가 되시나요? 점선으로 표시된 부분이 그래프를 그리면서 생략된 부분입니다. 원래는 계속 그래프가 이어져 나가겠죠.
이 그림을 통해서 왜 tan 주기가 π인지도 알 수 있습니다. 그렇죠? 4개의 정사각형의 그림(0 ~ π까지)이 계속 반복되고 있다는 것.
보이시죠? 안보이세요? 파란색선이랑 초록색선이랑 한 묶음, 빨간색선이랑 주황색선이랑 한 묶음이잖아요... 이제 이해 되셨죠?
주기라는 의미를 정확히 알고 계신다면 그 부분까지도 파악 하셨으로 것으로 생각됩니다.
